Kapitel 1E: Konstruktion utan tillgång till flyktpunkt

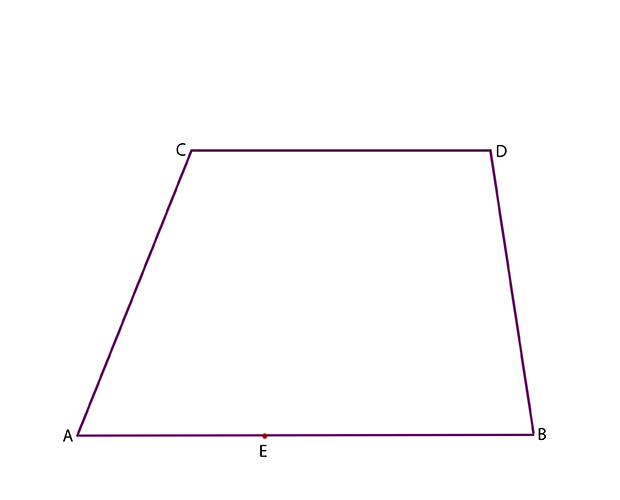
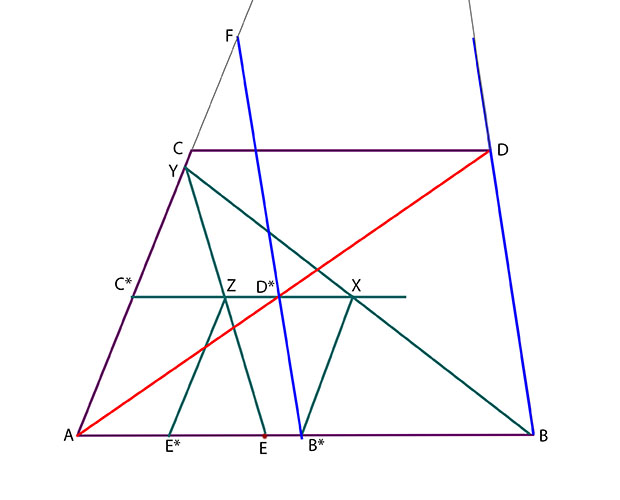
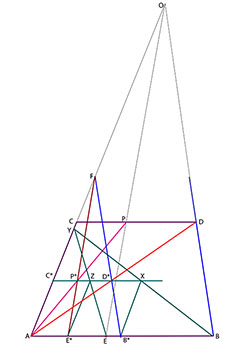
Vi startar med bilden av en rektangel ABCD med två sidor parallella med bildplanet och en punkt E på den närmaste av dessa sidor.

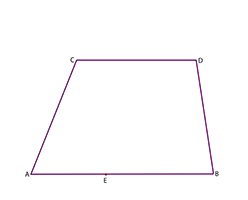
Genom den markerade punkten E går bilden av en linje som är parallell med rektangelsidorna vars bilder är AC och BD.
Denna linje konstrueras enkelt med hjälp av en flyktpunkt.

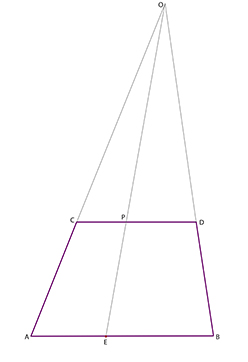
Förutsättningen för denna konstruktion är att man har utrymme att konstruera flyktpunkten O. Men konstnären måste i stort sett hålla sig inom det utrymme som ges av duken som han målar på. Frågan är nu hur han skall göra för att ändå konstruera punkten P, (utan att direkt konstruera flyktpunkten O).

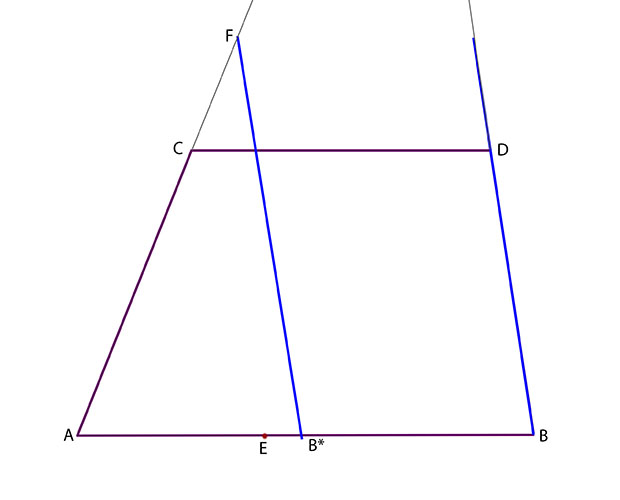
Börja med att förlänga sidorna AC och BD så långt det går inom det begränsade utrymme som står till buds.
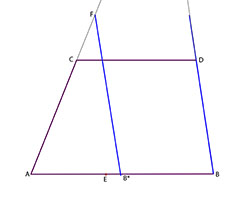
Välj sedan en punkt F på förlängningen av sidan AC. Drag den linje genom F som är parallell med sidan BD. Denna linje träffar sidan AB i punkten B*. I bilden är alltså de båda blåmarkerade linjerna parallella. Det innebär att triangeln FAB* är likformig med triangeln OAB. Man kan tänka på triangeln FAB* som en miniatyr av den stora triangeln OAB, som inte får plats på duken.

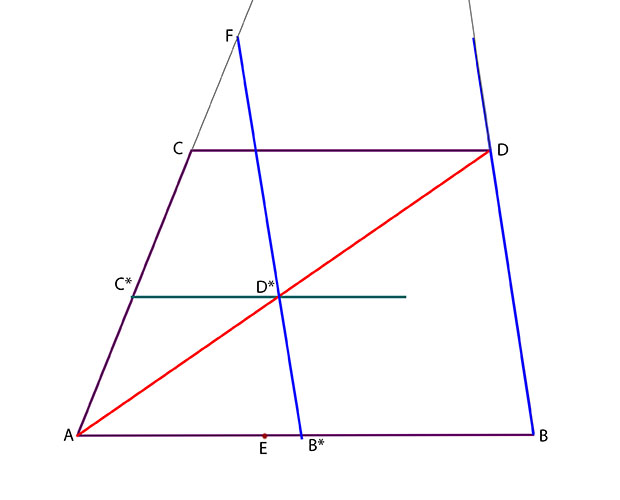
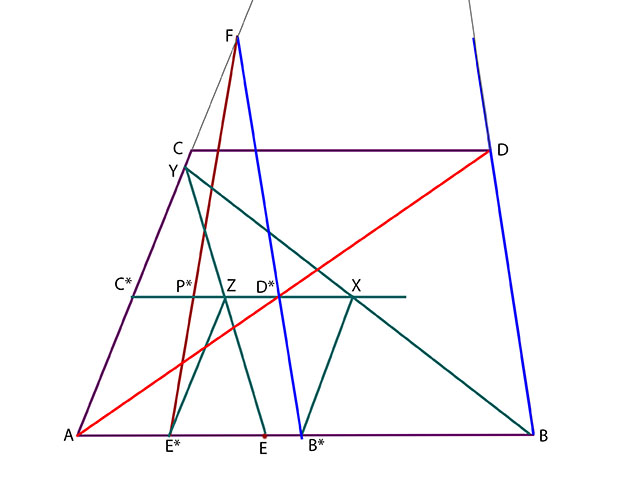
Nästa steg är att rita en miniatyr av parallellogrammen ABCD. Drag då diagonalen AD. DEn träffar linjen FB* i punkten D*. Drag genom D* en linje som är parallell med sidan AB. Denna linje träffar sidan AC i punkten C*. Det är klart att parallellogrammen AB*C*D* är likformig med ABCD.

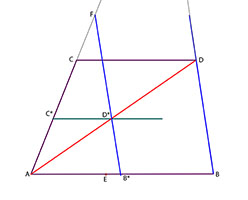
Konstruktionen ovan innebär att vi har avbildat parallellogrammen ABCD på den mindre parallellogrammen AB*C*D*. Vi vill nu konstruera den punkt E* som motsvarar punkten E. Den skall ha egenskapen att förhållandet mellan avståndet AE* och avståndet AB* är detsamma som avståndet mellan avstånden AE och AB.
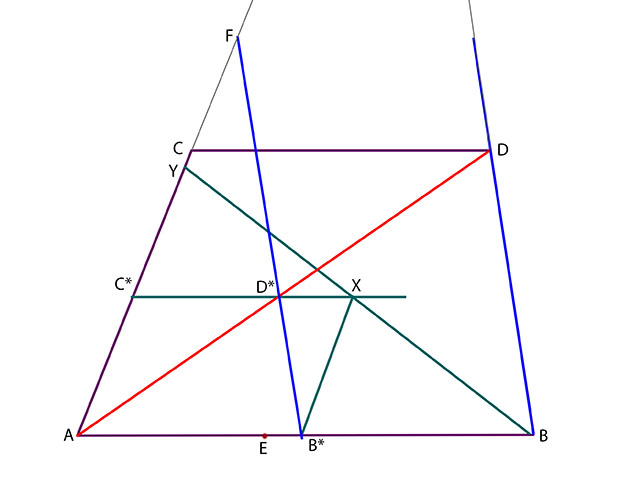
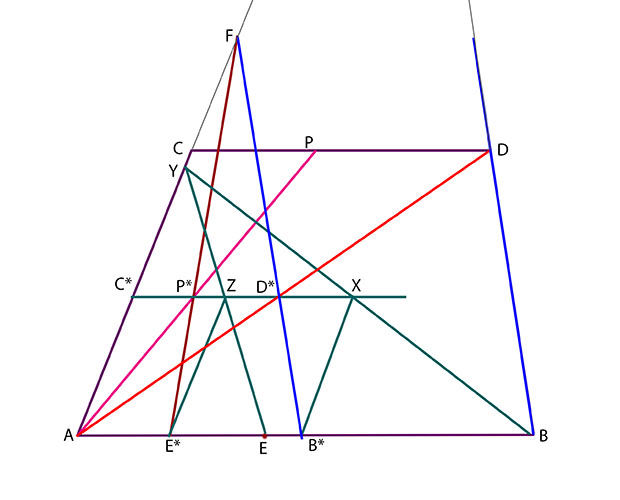
Det finns flera sätt att konstruera punkten E*. Här ett exempel:
Drag linjen från B* parallell med AC. Den träffar linjen C*D* i punkten X. Drag linjen BX. Den träffar linjen AC i punkten Y. Nu är trianglarna YAB och YC*X likformiga.

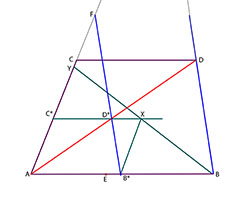
Drag linjen YE. Den träffar linjen C*D* i punkten Z. Drag slutligen linjen genom Z parallell med AC (och därmed B*X). Denna linje träffar linjen AB punkten E*. Detta är den önskade punkten. Det beror på att trianglarna YC*Z och YAE är likformiga, liksom trianglarna YC*X och YAB. Därför är C*Z/C*X = AE/AB, men eftersom C*Z=AE* och C*X=AB* enligt konstruktionen, så är även AE*/AB* = AE/AB, vilket var just vad vi ville ha.

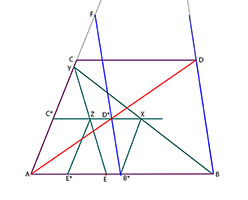
Drag nu linjen FE*. Den träffar linjen C*D* i punkten P*.

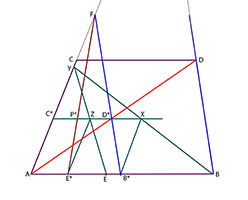
Drag nu till slut linjen AP*. Den träffar linjen CD i punkten P.
Detta är den sökta punkten.

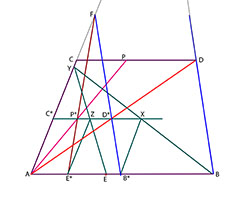
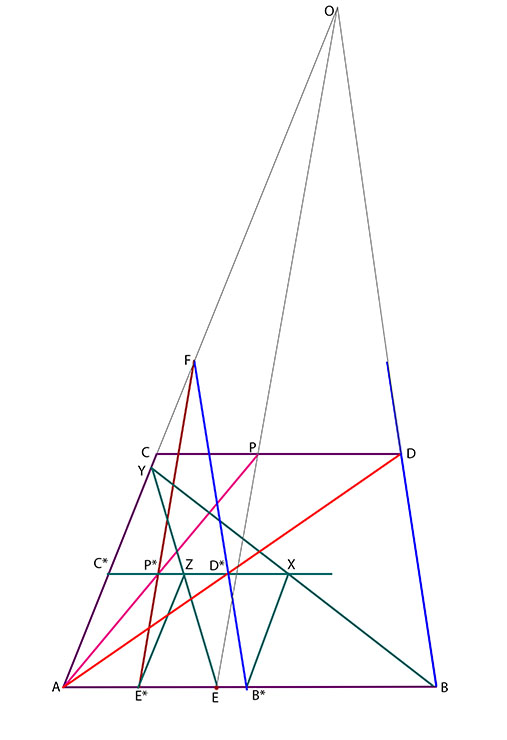
Enligt konstruktionen är nämligen triangeln FAB* likformig med OAB
och triangeln FAE* likformig med OAE.
Vidare är parallellogrammerna ABCD likformig med AB*C*D*
och AECP likformig med AE*C*P*. Därför är FC*P* likformig med OCP.
Saken är klar! (Därmed inte sagt att det är enkelt!)

Detta är för närvarande sista avsnittet!

Instruktioner: För att öppna ett avsnitt klicka på avsnittets rubrik. För att stänga avsnittet klicka på den röda texten i avsnittets slut. Du kan förstora alla bilder genom att klicka på dem. Förstorade bilder kan flyttas omkring med "drag and drop", dvs genom att du trycker ner musen på den förstorade bilden och flyttar musen. Släpp sedan upp musen där du vill ha bilden. Förstorade bilder stängs med ett klick på det lilla röda krysset uppe till vänster på bilden.