1 Om den centralperspektiviska bilden av en kvadrat.

1.1 Problembeskrivning

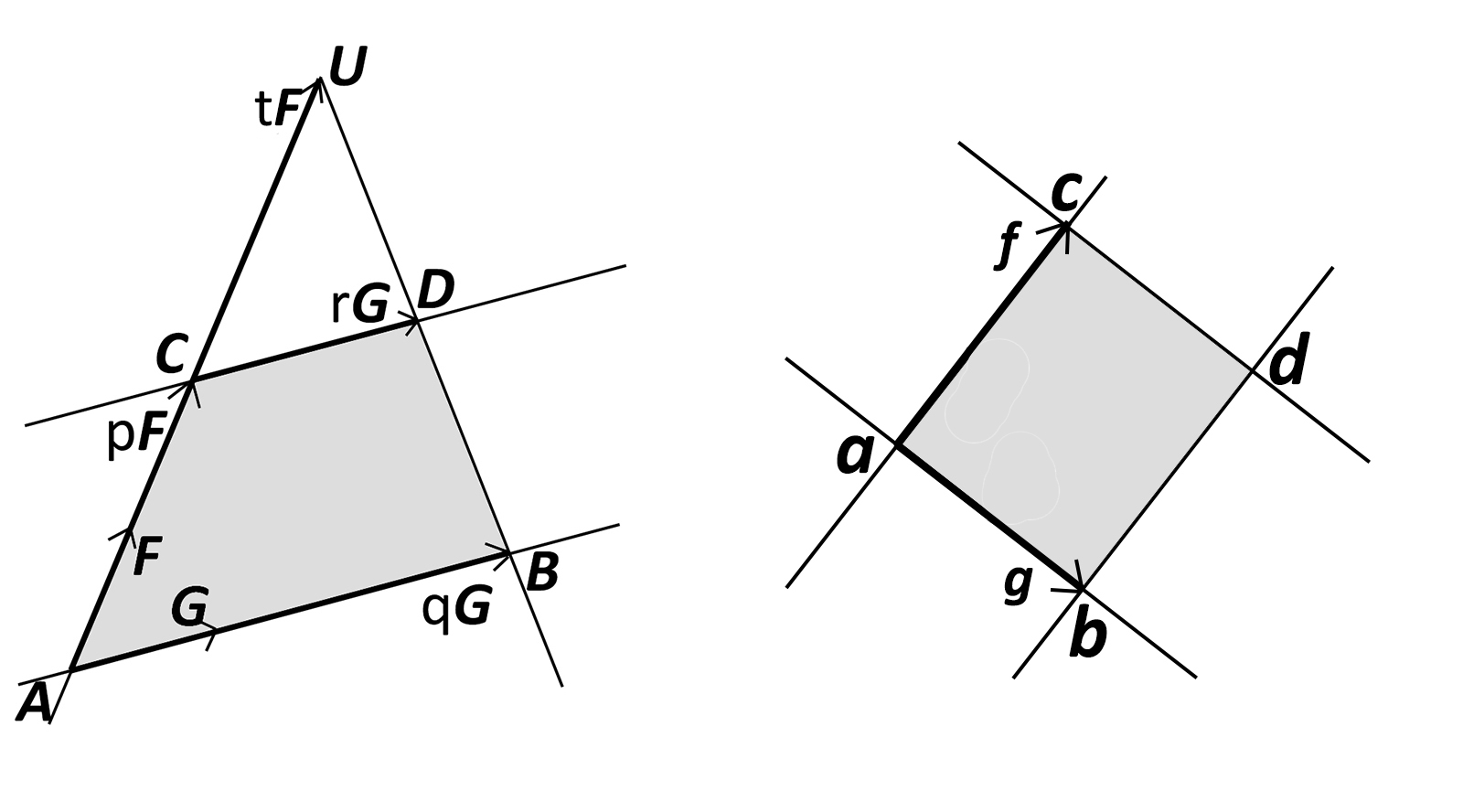
Vi tänker oss en rektangel i rummet med hörn i punkterna a,b,c,d. Sidornas riktningsvektorer betecknas med f och g enligt figuren nedan.
Vidare har vi en parallelltrapets med hörn i A,B,C,D, där sidorna AB och CD antas vara parallella, medan sidorna AC och BD inte är parallella. Deras förlängningar möts istället i punkten U. I figuren är G och F enhetsvektorer på sidorna AB respektive AC. Talen q och p betecknar alltså dessa sidors respektive längd, medan t betecknar avståndet från C till U.

Vi skall nu undersöka vilka villkor som måste vara uppfyllda för att den högra rektangelns centralperspektiviska bild skall vara parallelltrapetsen till vänster.Vidare skall vi se vilka tilläggsvillkor som behövs om rektangeln är en kvadrat.

1.2 Grundläggande formler

Vi inför koordinater för punkterna i de båda figurerna med hjälp av formeln för centralperspektivet. Om x är en punkt så är dess centralperspektiviska bild

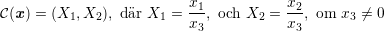
x x C(x) = (X1,X2 ), där X1 = -1, och X2 = -2, om x3 ⁄= 0 x3 x3

Vi har alltså sambandet

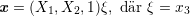
x = (X1, X2,1)ξ, där ξ = x3

Observera också att om två parallella linjer avbildas i två skärande linjer, så måste skärningspunkten vara bildlinjernas flyktpunkt och riktningsvektorn för dessa linjer ha tredje koordinat ≠0. I vårt fall måste alltså f = (f₁,f₂,f₃) , där f₃≠0. För flyktpunkten U gäller då

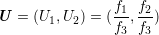
f f U = (U1,U2) = (-1,-2) f3 f3

Eftersom linjerna med riktningsvektor g = (g₁,g₂,g₃) avbildas i parallella linjer måste g₃ = 0. Om nu A = (A₁,A₂) och G = (G₁,G₂) så ger sambandet B = A + qG att

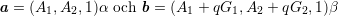
a = (A ,A ,1)α och b = (A + qG ,A + qG ,1)β 1 2 1 1 2 2

Eftersom g = b - a och g₃ = 0 så ger detta att α = β och därför också

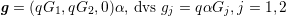g = (qG1, qG2,0)α, dvs gj = qαGj, j = 1,2

(1)

Eftersom f_j = U_jf₃,j = 1,2 får vi att

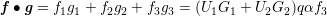
f ∙ g = f1g1 + f2g2 + f3g3 = (U1G1 + U2G2)qαf3

Nu är vinkeln mellan vektorerna f och g rät precis när f ∙g = 0. Det innebär att vår parallelltrapets är bild av en rektangel samtidigt som följande samband gäller:

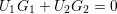
U1G1 + U2G2 = 0

Vi går nu vidare med syftet att undersöka vilka tilläggsvillkor som måste vara uppfyllda för att rektangeln skall vara en kvadrat. För det ändamålet skall vi ta fram en formel för vektorn f. Den formeln tillsammans med (1) kan vi sedan använda för att jämföra längderna av sidorna i rektangeln a,b,c,d.
På samma sätt som ovan har vi att

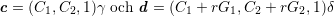
c = (C1,C2, 1)γ och d = (C1 + rG1, C2 + rG2,1)δ

Men vi har också att

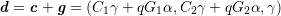
d = c + g = (C1γ + qG1α, C2γ + qG2α,γ )

Jämför vi dessa uttryck med varandra får vi att δ = γ och att

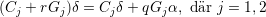
(Cj + rGj)δ = Cjδ + qGjα, där j = 1,2

Det betyder att rG_jδ = qG_jα,j = 1,2. Eftersom inte båda talen G_j,j = 1,2 kan vara noll, så ger detta att rδ = qα. Observera nu att likformighet ger att

-qt-- r = p+ t

Av sambandet rδ = qα följer då att

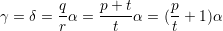
q- p+-t- p- γ = δ = rα = t α = (t + 1)α

Eftersom f = (f₁,f₂,f₃) = c - a , så får vi

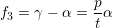
p- f3 = γ - α = t α

vilket till sist ger

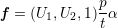f = (U1,U2,1 )pα t

(2)

1.3 Slutsatser

Vi har redan konstaterat att vår parallelltrapets är centralperspektivisk bild av en rektangel precis när

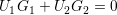U G + U G = 0 1 1 2 2

(3)

Man observerar att detta alltid är uppfyllt om flyktpunkten är origo dvs. om U = (0,0). Varje parallelltrapets vars icke-parallella linjer skär varandra i origo är alltså bild av en rektangel.

Om rektangeln är en kvadrat måste sidorna vara lika långa. Längden av g är (enligt formel (1) )

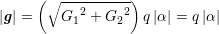
( ∘ ---------) |g| = G12 + G22 q|α| = q |α |

eftersom G är en enhetsvektor. Enligt (2) är längden av f lika med

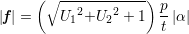
( ∘ -----------) |f| = U12+U22 + 1 p-|α | t

Ett avgörande villkor för att parallelltrapetsen skall vara bild av en kvadrat är alltså att (3) gäller och att

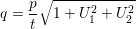p∘ -----2-----2 q = t- 1 + U1 + U2

(4)

Om parallelltrapetsen är bild av en kvadrat måste exempelvis alltid q ≥ p∕t . Om flyktpunkten ligger i origo måste q = p∕t.