Centralperspektivet är både en teoretisk och en praktisk metod. Den centrala idén är konstruktionen av flyktpunkter.
Detta avsnitt är ett försök att förklara centralperspektivets teoretiska sida och särskilt just begreppet flyktpunkt.
Så här kan man beskriva centralperspektivet:
Konstnären placerar sitt skarpa öga (bara ett öga) i en viss punkt, spänner upp
en (transparant) duk framför sig och tecknar av motivet. Från en punkt i
motivet löper en tänkt linje till konstnärens öga. Där denna linje träffar
duken sätter konstnären en punkt. Detta är bilden av verklighetens punkt.
Konstruktionsmetoden kallas centralperspektivet.
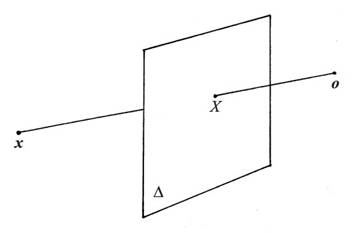
I figuren markerar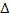 
målardukens plan, medan
o är rummets origo, där konstnärens öga tänks vara placerat. Vidare är x en punkt i rummet.
Punkten X är skärningspunkten mellan målarduken och linjen genom x och origo.
Punkten X är då den centralperspektiviska bilden av punkten x.
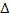Observera att målarduken är tänkt att ha
oändlig utsträckning, så teckningen visar bara en begränsad del av duken.
Vissa punkter saknar centralperspektivisk bild. Det gäller rummets origo, men också alla punkter i det plan genom origo,
som är parallellt med planet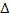
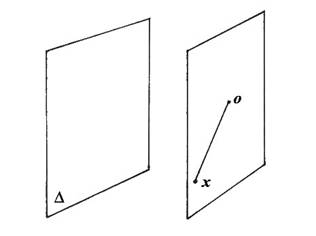
Linjen genom origo och punkten x skär aldrig planet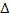
Punkten har därför inte någon centralperspektivisk projektion.
Flyktpunkter
Ritar man bilden (alltså den centralperspektiviska bilden) av en rak väg, så kommer
man att upptäcka att bilden av vägens på kanter löper samman i en punkt. Detta
är vägkantens flyktpunkt. Alla parallella linjer har en gemensam flyktpunkt.
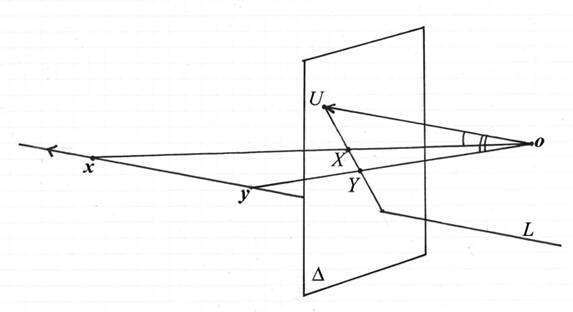
Bilden visar en linje L .
Pilen på linjen markerar linjens riktning. Genom origo o har man dragit en linje som är parallell med
L och den träffarmålarduken i punkten U .
När en punkt rör sig bort från origo längs linjen L så kommer dess centralperspektiviska bild att närma sig U.
Man får en antydan om varför i figuren. De markerade vinklarna vid origo blir mindre och mindre ju längre bort punkten
ligger. Vinkeln xoU (markerad med enkel båge) är som synes mindre än yoU (dubbel båge).
Flyktlinjer
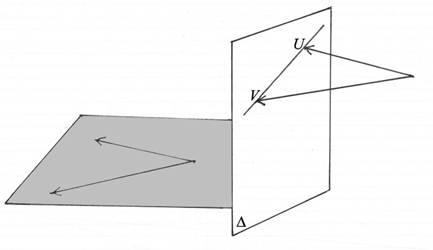
Ritar man två linjer i ett plan kommer dessa linjers flyktpunkter att ligga på en
linje. Vi kallar den linjen för planets flyktlinje. I figuren är planet
markerat med grå färg. Flyktpunkterna för två linjer är markerade i målardukens
plan. Linjen mellan dessa två punkter är planets flyktlinje.
Konstnären ritar i princip bara av det som finns bakom den transparanta målarduken. I denna framställning höjer vi oss
suveränt över sådan praktiska hänsyn. Vi låter alla punkter i rummet
avbildas på målarduken. Enda undantaget är de punkter som ligger i planet genom
origo som är parallellt med dukens plan. Vi får tänka oss att konstnärens öga
är som en sådan där kamera som ser hela horisonten runt.
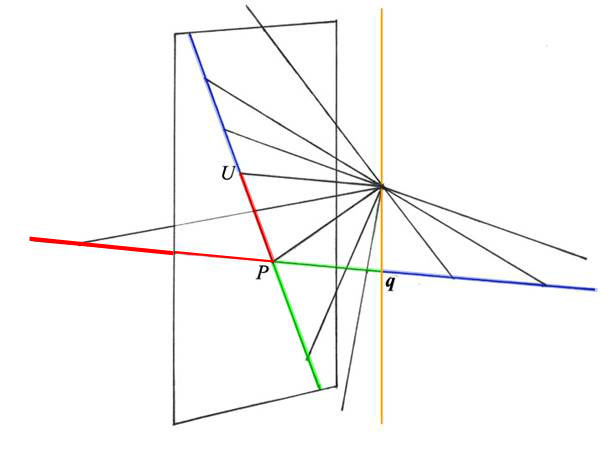
I bilden visas en linje och dess bild på duken. Punkten P
är linjens skärningspunkt med duken, medan U är linjens flyktpunkt.
Den del av linjen som ligger bakom målarduken är markerad med rött. Samma färg
används för bilden på duken. Den orange-färgade lodlinjen markerar den linje genom
origo som är parallell med duken. Den skär linjen i punkten q. Denna punkt har,
som vi sagt ovan, ingen bild på målarduken. Den del av linjen som ligger till höger om q
är blåmarkerad liksom dess bild på duken. Mellanrummet mellan P
och q och dess bild på duken är markerat med grön.
Om man tänker sig att man följer en
punkt från höger till vänster. Vi börjar ”oändligt” lång till höger med en punkt.
Medan punkten rör sig åt vänster kommer dess bild att röra sig uppåt från
punkten U längs den blå linjen på duken. När punkten närmar
sig q kommer bilden att försvinna uppåt på duken. När väl
punkten på linjen har passerat över punkten q dyker bilden upp ”oändligt” långt nere på duken och
följer sedan den gröna linjen upp mot punkten P. Därefter passerar punkten genom duken och bilden fortsätter upp mot
U. Flyktpunkten representerar så att säga punkter som ligger ”oändligt” långt borta på linjen,
(till vänster eller höger). På likande sätt representerar punkten q
”oändligt” avlägsna punkter på bilden av linjen.
Stäng "Från oändlighet till oändlighet"
Sammanfattning
Alla parallella linjer som inte är parallella med målarduken har en gemensam flyktpunkt!
I skaran av parallella linjer finns det en som passerar genom rummets origo
o och den träffar målarduken i flyktpunkten!
Alla linjer i ett plan som inte är parallellt med duken har sina flyktpunkter på en linje, planets flyktlinje
och alla parallella plan har samma flyktlinje!
Stäng "Beskrivning av centralperspektivet"