Kapitel 1D: Variationer och tillägg

Om man startar med bilden av en kvadrat eller en parallellogram kan man konstruera de parallella linjeparens flyktpunkter genom att helt enkelt förlänga sidorna.

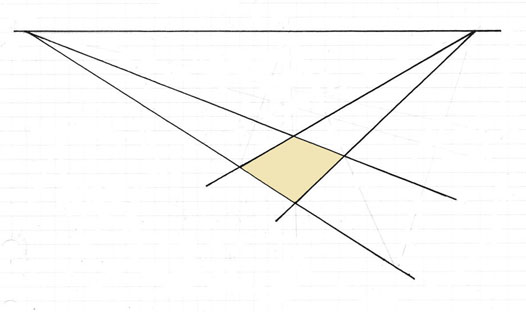
Linjen genom de två flyktpunkterna är flyktlinjen för det plan i vilket parallellogrammen ligger. Sedan kan man konstruera ett rutnät genom att först finna ena diagonalens flyktpunkt och därefter fortsätta konstruktionen ungefär som i föregående avsnitt.

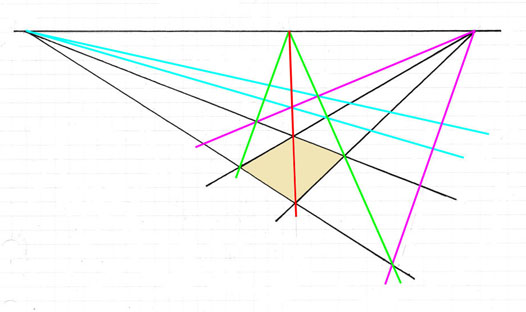
I denna bild har den röda linjen (diagonalen) ritats först. Dess skärning med flyktlinjen är diagonalens flyktpunkt. Sedan har linjerna ritats i följande ordning: grönt, magenta, cyan. Om den givna parallellogrammen ligger i ett lutande plan kommer flyktlinjen inte horisontell . Konstruktionen blir i princip densamma.

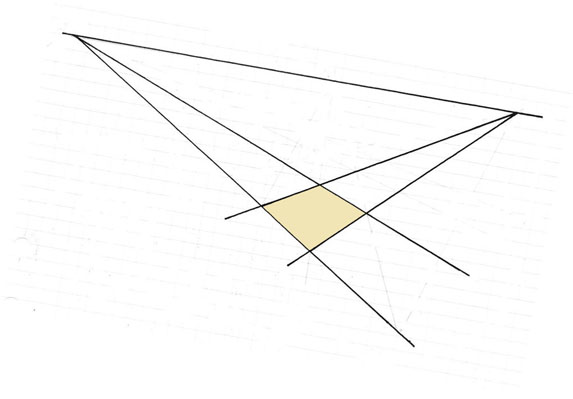
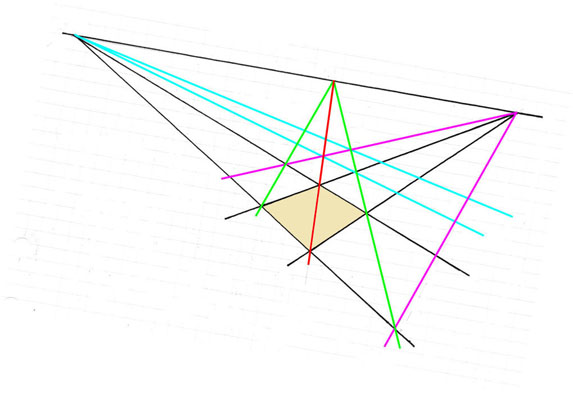
Stäng "Alternativ konstruktion av rutnät"

Först lite terminologi:

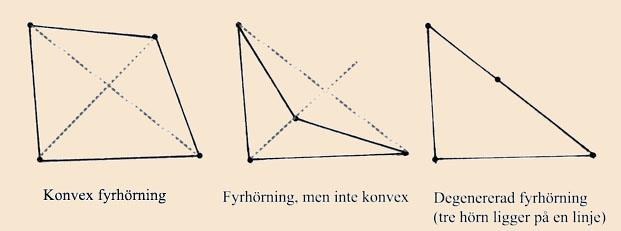
En fyrhörning begränsas av fyra linjer vilka skär varandra i fyra punkter, hörnen. Tre av hörnen får inte ligga på en linje. Om fyrhörningens båda diagonaler skär varandra inne i fyrhörningen sägs fyrhörningen vara konvex.
Den centralperspektiviska bilden av en kvadrat måste vara en konvex fyrhörning. Det beror på att en kvadrat är konvex och på att diagonalerna i kvadraten avbildas på diagonalerna i bilden.

Låt oss vända på frågan och undersöka om varje konvex fyrhörning är bild av en kvadrat. Till en början kan man visa att varje konvex fyrhörning är bild av en parallellogram. Diskussionerna under rubriken ”Alternativ konstruktion av rutnät” ovan, visar nämligen att varje konvex fyrhörning är bild av en parallellogram. Motstående sidolinje i fyrhörningen är nämligen antingen parallella (i vilket fall urbildens motsvarande sidor också är parallella) eller också skär motstående sidolinjer varandra i en punkt som då kan ses som flyktpunkt för två parallella linjer i urbilden.

Däremot är inte varje konvex fyrhörning inte bild av en kvadrat. Se på följande exempel:

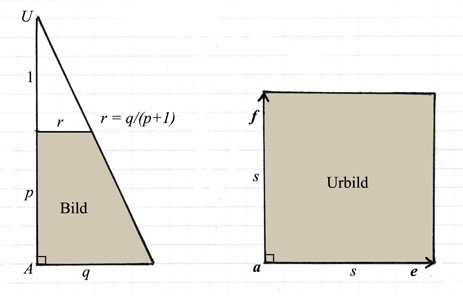
Formeln för storheten r är en konsekvens av ett likformighetsargument!

Antag att det som betecknas som Bild verkligen är en centralperspektivisk bild av det som kallas Urbild. Då måste linjen genom A och U vara lodlinjen genom projektionsdukens centrum. För om Urbilden ligger till vänster om lodlinjen blir bilden av vinkeln vid a (alltså vinkeln vid A) mindre än 90 grader. Om Urbilden istället ligger till höger om lodlinjen blir vinkeln större än 90 grader. (Se bilden nedan!)

Om vi antar att Urbilden ligger bakom duken måste så kommer bilden av f att vara kortare än bilden av e, dvs p <= q. Men i bilden är det inte så! Därför är Bild inte bilden av någon kvadrat (som ligger bakom projektionsduken).

Klicka här för ett alternativt, mer räknemässigt bevis.

En utvidgad utredning om utseendet hos bilden av en kvadrat finner du i följande pdf-fil:
Om den centralperspekiviska bilden av en kvadrat
eller i html-format:
Om den centralperspekiviska bilden av en kvadrat

Stäng "Är detta bilden av en kvadrat?"

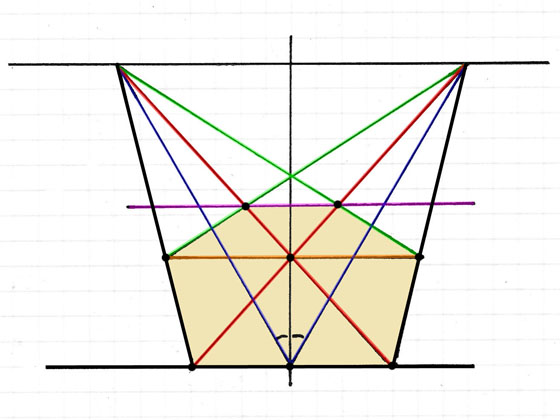
I den första figuren visas en regelbunden sexhörning. Den markerade vinkeln är 30 grader. De båda blå och de båda röda linjerna är parallella med motsvarande sidor i sexhörningen. Deras bilder har därför samma flyktpunkter. Det finns alltså två par om vardera fyra linjer. Till varje par hör en flyktpunkt.

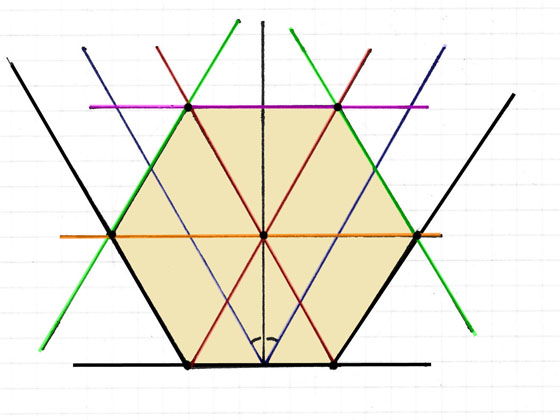
Nästa bild visar konstruktionen av flyktpunkterna för de två paren av fyra parallella linjer. Först dras de båda vågräta linjerna och sedan lodlinjen. Sedan Konstrueras de båda blå linjerna så att de båda markerade vinklarna blir 30 grader. De blå linjerna träffar den övre vågräta linjen (horisontlinjen) i två punkter. Det är önskade flyktpunkterna. Därefter dras linjerna i följande ordning. Först dras de båda svarta sneda linjerna. Därefter de båda röda linjerna. Genom deras skärningspunkt (på lodlinjen) dras en vågrät linje (orange). Från denna linjes båda skärningspunkter med de båda sneda svarta linjerna dras de två gröna linjerna. ' Slutligen förenas dessa linjers skärningspunkter med de båda röda linjerna med den vågräta magenta linjen.

Stäng "Konstruktion av en regelbunden sexhörning"